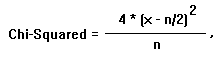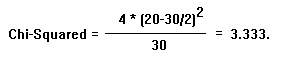|
In the evaluation of ABX Double Blind Test results, statistics are used to get
as much information as possible from each test. The statistical methods
reviewed here are by no means the only ones available for use with an ABX
Double Blind Comparator. They are however the methods that we at the ABX
Company have found useful in ABX Double Blind Comparisons. Experienced
researchers may utilize methods beyond the scope of this paper. |
|
One traditional approach to audibility thresholds defined the threshold point
as midway between all correct (100%) and guessing (50%). Thus less than 75%
correct indicated the effect was not detected by the listeners. With
statistical evaluation, ABX Double Blind Comparisons can show audible
differences with as little as 51% correct, provided the experiment is
carefully designed.
|
|
The statistics to bring this high level of resolution are elementary. The
discussion to follow can serve both as an explanation for those new to
statistics or as a reminder to statisticians who don't use these simple
methods regularly.
|
|
WHAT IS BEING TESTED ?
|
|
Although novel experiments may be designed to utilize the Double Blind
features of the ABX Comparator System, it was designed initially for
comparisons of audio components. In this application, the ABX Company has
adopted the following definitions:
|
|
It is important not to confuse SUBJECT and LISTENER. Listeners thinking their
ears are on trial may be intimidated and thereby not do their best. This
caution is worth explaining at the beginning of each test.
|
|
Since the randomization of the ABX Comparator is internal, the EXPERIMENTER
and the LISTENER may be the same person. With the ABX Comparator Double Blind
tests may be done by a single person working alone.
|
|
MISSING A FEW
|
|
Listeners don't have to be correct on each and every response to show that the
effect being tested is detectable. When some responses are incorrect, the
science of statistics is called upon to show the responses do relate to the
effect being tested. The statistics are basic, so basic that they are rarely
explained in practical terms in statistics texts.
|
|
WHAT IS p ?
|
|
Statistics is a science of probabilities. There are no absolute tests of
absolute proof. The result of a statistical analysis is also a probability.
Whether a result is random or not random is stated statistically as the
likelihood of the result being random. A result's randomness is determined by
comparing the experimental result with results that have been theoretically
studied. These reference points are called "distributions". To test if an
ABX Double Blind score is random or a significant event, the score would be
compared with a known distribution.
|
|
Tossing a single coin repeatedly is statistically identical to the listeners
score in an ABX Double Blind Comparison. The coin is random; its distribution
is well known. In a very large number of tosses the head comes up half the
time. If the listeners just guessed in an ABX Comparison, the score would
likewise be 50%. If the score is above 50%, it may be random or not. Which
depends on the number of trials run. Generally the evidence that the score
was not like random guessing is stronger the more trials are run, although
advanced researchers may be able to calculate an optimum number of trials in
certain circumstances. We at the ABX Company have found sixteen trials to be
fairly sensitive without an undue burden on the listeners.
|
|
If a coin is tossed sixteen times, there won't always be exactly 8 heads.
Five to eleven heads may occur quite frequently in each group of sixteen
tosses. If twelve heads occur in sixteen tosses, the coin may be out of
balance.
|
|
The dividing line is between eleven and twelve because the coin toss
distribution has been compared to other known distributions. The closest ones
are the Chi-Squared Distribution and the Binomial Distribution. The Chi-
Squared Test is easy to use by a simple calculation and a table of Chi-Squared
valued and the corresponding probability values, but is approximate for small
scores. The Binomial Distribution Test is exact but tables are not readily
available for large numbers. The ABX Comparator User's Manual includes an
exact Binomial Distribution Table for up to 40 trials. The ABX Company has
prepared a Binomial Table for up to 600 trials. It is a 2 inch thick
printout. [This was written in 1982.]
|
|
USING THE BINOMIAL TABLE
|
|
The table is easy to use. If, for example, the experiment's result was 20 X's
out of 30 correctly identified, 20 is found across the top of the page and 30
at the side. The number at the row column intersection is the probability
this score could have occurred in a coin toss or guessing situation. For
20/30, the probability listed in the table is 0.049. This means that in 100
random fair coin toss experiments consisting of 30 unknowns, a score of 20/30
or better would be expected to happen almost five times, but no more. Thus
20/30 is a fairly rare event. In a scientific report this would be stated:
67% correct (p=0.049).
|
|
In rigorous scientific experiments the value of p is chosen in advance as a
goal. The most common p value thus set is 0.05. Lower values are sometimes
sought and achieved, but higher values are almost never tolerated. It would
be unwise to report an audibility result if p is not below 0.05.
|
|
USING CHI-SQUARED
|
|
In the same 20 X's correct out of 30 X's example, a value of Chi-Squared is
calculated by the formula below. The probability of the Chi-Squared value is
determined from the Chi-Squared Table. In the case of an ABX Double Blind
Comparison, the Chi-Squared value is:
|
|
In the ABX Double Blind Comparison the goal is to statistically disprove the null hypothesis to confirm the hypothesis.
|
|
When an individual ABX Comparision is completed, the responses are checked
against the key in the ABX Comparator in ANSWER mode. The number of correct
responses is compared to the number of response attempts to give a score such
as the example of 20 correct out of 30 attempts, which we have written briefly
as a fraction or a percentage: 20 / 30 = 67%. The score is then compared
with the probability table from which the probability that it is a random
score is determined. Thus the result is stated: 20 / 30 = 67% (p = 0.049).
This literally means that the score (20/30) is probably not random except for
a 0.049 chance that it is random. Thus the result of the experiment is that
the null hypothesis is not true except for a 0.049 chance it is true, or in
audiophile terms, A sound different from B except for a 4.9% chance that they
are the same.
|
|
Note that no matter what score is achieved, A = B cannot be proven. That is
the ABX Double Blind Comparison can never be used to prove two audio
components sound the same. The notion that ABX can prove components sound the same is a common misconception about ABX.
|
|
A second common misconception about ABX is the claim that an ABX test result
is not a preference: it doesn't tell which audio component sounds better.
While literally true, if an ABX test confirms a difference is heard, selecting
one's preference is easy and completely justified.
|
|
If the score had been random, 19 / 30 = 63% (p = 0.1), all that could be
reported is the experimentor failed to disprove the null hypothesis. No
further conclusion could be reached about the similarity or difference of
component A and component B from this Double Blind experiment. Of course a
near miss score like 19 / 30 may tempt the experimenter to attempt more trials
in the hope of the new score and the combined score being significant.
|